PRL published: Shaping electron wave functions in a carbon nanotube with a parallel magnetic field

We're happy to announce that our manuscript "Shaping electron wave functions in a carbon nanotube with a parallel magnetic field" has been published as Editor's Suggestion in Physical Review Letters.

When a physicist thinks of an electron confined to a one-dimensional object such as a carbon nanotube, the first idea that comes to mind is the „particle in a box“ from elementary quantum mechanics. A particle can behave as a wave, and in this model it is essentially a standing wave, reflected at two infinitely high, perfect barrier walls. The mathematical solutions for the wave function describing it are the well-known half-wavelength resonator solutions, with a fundamental mode where exactly half a wavelength fits between the walls, a node of the wave function at each wall and an antinode in the center.

In this publication, we show how wrong this first idea can be, and what impact that has. In a carbon nanotube as quasi one-dimensional system, an electron is not in free space, but confined to the lattice of carbon atoms which forms the nanotube walls. This hexagonal lattice, the same that also forms in planar form graphene, is called bipartite, since every elementary cell of the lattice contains two carbon atoms; one can imagine the nanotube wall as being built out of two sub-lattices, with one atom per cell each, that are shifted relative to each other. Surprisingly, the hexagonal bipartite lattice does not generally support the half-wavelength solutions mentioned above, where the electronic wave function becomes zero at the edges. In each sublattice, we can only force the wave function to zero at one end of the nanotube "box"; its value at the other end remains finite. This means that the wave function shape for each of the two sublattices is more similar to that of a quarter wavelength resonator, where one end displays a node, the other an antinode. The two sublattice wave functions are mirrored in shape to each other, with node and antinode swapping position.

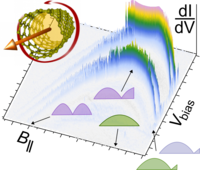
When we now apply a magnetic field along the carbon nanotube, a magnetic flux enters the nanotube, and the boundary conditions for the electron wave function change via the Aharonov-Bohm effect. Astonishingly, its shape along the carbon nanotube can thereby be tuned between half-wavelength and quarter-wavelength behaviour. This means that the probability of the trapped electron to be near the contacts changes, and with it the tunnel current, leading to a very distinct behaviour of the electronic conductance. It turns out that our measurement and the corresponding calculations are agreeing very well. Thus, our work shows the impact of a non-trivial host crystal on the electronic behaviour, important for many novel types of material.

"Shaping electron wave functions in a carbon nanotube with a parallel magnetic field"
M. Marganska, D. R. Schmid, A. Dirnaichner, P. L. Stiller, Ch. Strunk, M. Grifoni, and A. K. Hüttel
Physical Review Letters 122, 086802 (2019), Editor's Suggestion; arXiv:1712.08545 (PDF, supplementary information)